Some of the figures in this post are more easily read in light mode rather than dark mode. When time allows I will find suitable replacement images.
Back in May 2020 I released a video on YouTube for the HackSeq event:
But I figure I could give some written description as well, which is what the rest of this blog post covers.
A graph is a 2-tuple containing a set of edges and a set of vertices, and the set of edges is a subset of the cartesian product of the set of vertices with itself. We can think the vertices as ‘things’ and the set of edges as a binary relation between them.
Sometimes graphs are called “networks” when either the vertices (often called “nodes” when discussing networks) or edges have additional attributes, however this usage is not universally accepted. Three common properties of graph edges are whether they are directed, signed, or weighted. In the case of directed edges, some sort of ‘directionality’ is associated with the edges, and we’d say that (u,v) and (v,u) are considered distinct for two vertices u and v from the graph. A graph with directed edges is called a directed graph or a digraph. In the case of signed edges, each edge is assigned a ‘positive’ or ‘negative’ value, and we call such a graph a signed graph. In the case of weighted edges, each edge is assigned a numerical value, and we call such a graph a weighted graph. If a graph doesn’t have directed, signed, or weighted edges and doesn’t have multiple edges for any given pair of vertices, then it is called a simple graph.
A graphlet is a specific type of graph, inheriting all the properties of graphs but also being a weakly-connected induced subgraph. For a graph to be subgraph, there exists another graph such that the subgraph’s vertex set is a subset of the other graph’s vertex set and the subgraph’s edge set is a subset of the other graph’s edge set. A subgraph being induced can be thought of procedurally, by first selecting any subset of the vertices and then also selecting all edges that connect those selected vertices. The property of weakly-connected can be considered for any graph, and means that there exists a path between any pair of vertices in the graph.
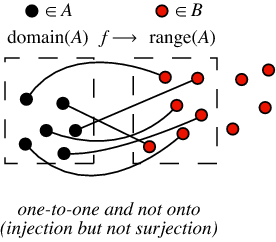
A function is injective if it satisfies that f(x)=f(y) implies that x=y.
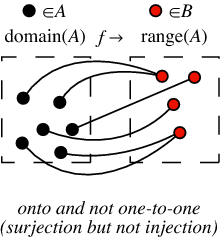
A function is surjective if it satisfies for any element b in the image that there exists an element a of the domain for which b=f(a).
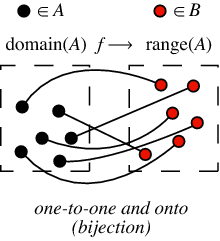
A bijection is a function that is both injective (one-to-one) and surjective (onto) from one set to another (these two sets can be the same set).
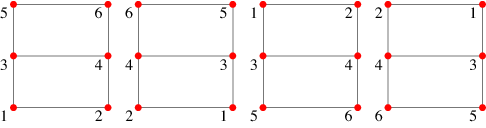
A graph isomorphism is a bijection f between two graphs (which can be the same graph in the case of graph automorphisms) such that any two vertices u and v in the first graph are adjacent if-and-only-if f(u) and f(v) are adjacent.
A graph automorphism is a graph isomorphism where the domain graph and the image graph are the same graph.
An equivalence relation is a binary relation that is reflexive, symmetric, and transitive. An equivalence class is a subset of a set such that all members of the subset adhere to an equivalence relation. A (vertex) orbit automorphism is an equivalence class from the vertex set of a graph under the action of a graph automorphism. Multiple graph automorphisms are possible, and the set of all automorphisms with composition of permutations of the vertex set is called a permutation group.
Since graphlets are graphs, and orbit automorphisms can be found within graphs, we can find orbit automorphisms within graphlets. The idea behind enumeration of orbit automorphisms of graphlets is to count the number of times each vertex of a graph participates in each orbit automorphism of each graphlet from a set of graphlets. While each finite graph has a finite number of distinct (i.e. mutually non-isomorphic) graphlets, considering every conceivable graphlet would be computationally infeasible. Instead of considering all graphlets of a graph, a constraint is often imposed where graphlets containing only 2-3 vertices are considered.
Enumeration of orbit automorphisms of graphlets has been used to characterize correlation networks of coexpression of genes, and characterize the role of traders in the world trade network.