A Rust Implementation of the Poisson Binomial Probability Distribution

The probability mass function of the Poisson binomial distribution is given by

\[\sum_{A \in F_k} \prod_{i \in A} p_i \prod_{j \in A^c} (1 - p_j)\]

where \(F_k\) is the set of all subsets of \(k\) integers that can be selected from the set \(\{ 1, \ldots, n \}\). This expression does not by itself suggest one algorithm over another due to the cummutativty and associativity of the operators involved.

Wikipedia gives pseudocode for computing the probability mass function for the Poisson binomial distribution via what it terms the “direct convolution algorithm”.

fn dc(p: &[f64]) -> Vec<f64> {
    let n = p.len();
    let mut pmf: Vec<f64> = vec![1.0]; // PMF array with size 1, initialized to 1

    for i in 0..n {
        // Create a new next_pmf array with size i + 2
        let mut next_pmf: Vec<f64> = vec![0.0; i + 2]; 

        // Calculate the first element of next_pmf
        next_pmf[0] = (1.0 - p[i]) * pmf[0];

        // Calculate the last element of next_pmf if within bounds
        if i < pmf.len() {
            next_pmf[i + 1] = p[i] * pmf[i];
        }

        // Update the rest of next_pmf
        for k in 1..=i {
            next_pmf[k] = p[i] * pmf[k - 1] + (1.0 - p[i]) * pmf[k];
        }

        // Update pmf for the next iteration
        pmf = next_pmf;
    }

    pmf
}

Let’s try to use the algorithm.

// Example usage
let p: Vec<f64> = vec![0.1, 0.2, 0.3, 0.4];
let pmf: Vec<f64> = dc(&p);
println!("{:?}", pmf);

[0.3024, 0.4404, 0.2144, 0.0404, 0.0024000000000000007]

We can also double check that the result resembles a probability by checking if the sum of the probabilities is in fact equal to unity.

let sum_check: f64 = pmf.iter().sum(); // Calculate the sum of the PMF values
println!("Sum of PMF: {}", sum_check);

Sum of PMF: 1

We can also define the cumulative distribution function (CDF) as the cumulative sum of the PMF.

fn compute_cdf(pmf: &[f64]) -> Vec<f64> {
    let mut cdf: Vec<f64> = Vec::with_capacity(pmf.len());
    let mut sum = 0.0;

    for &prob in pmf {
        sum += prob;
        cdf.push(sum);
    }

    cdf
}

Here is an example of using the CDF.

let cdf: Vec<f64> = compute_cdf(&pmf);
println!("CDF: {:?}", cdf);

CDF: [0.3024, 0.7428, 0.9572, 0.9976, 1.0]

Often we will want to be able to sample from such a probability distribution. Here is a function which implicitly relies on the inverse transform theorem.

:dep rand
use rand::Rng;

fn sample_from_distribution(cdf: &[f64]) -> usize {
    let mut rng = rand::thread_rng();
    let random_value: f64 = rng.gen(); // Generate a uniform random value between 0 and 1

    cdf.iter()
        .position(|&x| random_value <= x)
        .unwrap_or(cdf.len() - 1) // If not found, return the last index
}

Now let us take some samples.

let num_samples = 10000;

let samples: Vec<usize> = (0..num_samples)
        .map(|_| sample_from_distribution(&cdf))
        .collect();


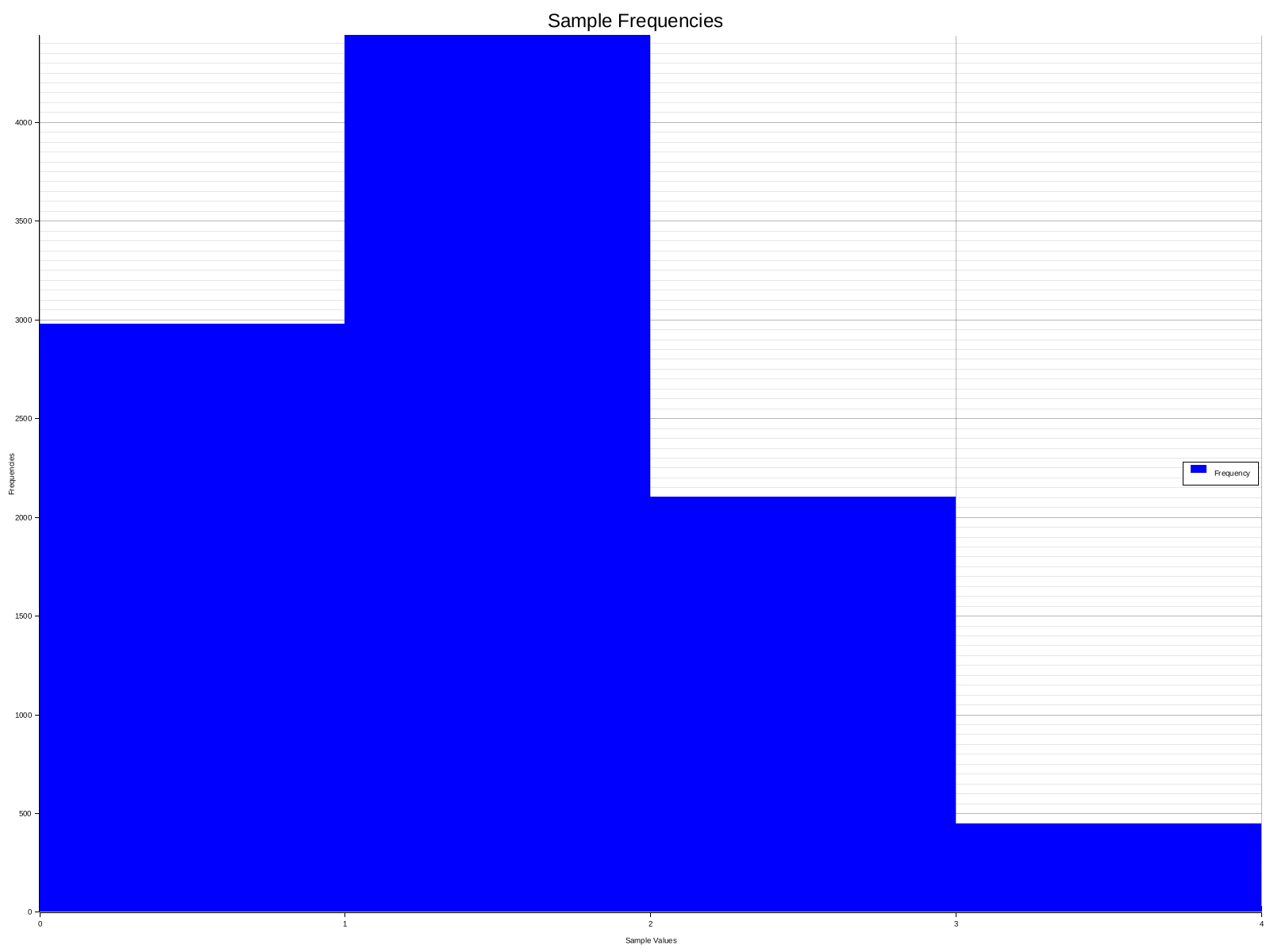
println!("Samples: {:?}", samples);

Samples: [2, 2, 2, 1, 0, 1, 1, 2, 1, 0, 1, 0, 0, 2, 0, 1, 1, 0, 1, 0, 2, 2, 0, 1, 0, 2, 0, 2, 2, 2, 0, 1, 1, 0, 2, 1, 1, 2, 3, 1, 0, 0, 0, 2, 2, 0, 1, 0, 1, 3, 1, 2, 1, 1, 2, 2, 0, 2, 1, 0, 2, 1, 1, 0, 0, 2, 1, 1, 1, 0, 1, 2, 0, 3, 1, 1, 1, 2, 0, 0, 1, 2, 0, 1, 1, 0, 1, 2, 1, 0, 1, 2, 2, 1, 3, 0, 3, 1, 2, 2, 2, 1, 0, 0, 1, 2, 1, 3, 0, 0, 1, 1, 1, 1, 2, 0, 1, 0, 0, 0, 1, 0, 2, 0, 2, 0, 2, 0, 0, 0, 0, 1, 2, 1, 2, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 2, 0, 1, 0, 1, 1, 1, 0, 0, 1, 2, 2, 0, 2, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 2, 0, 2, 0, 2, 1, 1, 3, 1, 2, 0, 0, 1, 1, 2, 2, 3, 2, 1, 1, 0, 1, 1, 1, 2, 1, 1, 2, 1, 0, 1, 0, 2, 1, 0, 0, 2, 1, 0, 1, 1, 2, 2, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 3, 1, 0, 1, 2, 4, 1, 4, 0, 1, 1, 2, 1, 0, 1, 1, 1, 1, 0, 2, 2, 1, 1, 0, 1, 2, 1, 2, 0, 1, 0, 1, 1, 0, 1, 2, 0, 1, 1, 1, 0, 2, 2, 1, 1, 1, 0, 2, 2, 1, 0, 0, 0, 0, 2, 0, 2, 2, 1, 1, 1, 0, 1, 2, 4, 2, 2, 1, 1, 1, 2, 1, 2, 1, 0, 4, 0, 0, 1, 0, 1, 1, 1, 1, 2, 3, 0, 1, 2, 1, 0, 2, 0, 1, 2, 1, 2, 3, 0, 1, 1, 1, 2, 1, 0, 0, 0, 2, 1, 1, 0, 2, 0, 1, 1, 0, 0, 1, 2, 1, 0, 1, 2, 2, 2, 2, 2, 2, 0, 2, 1, 0, 0, 2, 0, 2, 2, 0, 1, 1, 1, 1, 2, 2, 1, 0, 1, 1, 1, 3, 2, 2, 0, 0, 1, 2, 2, 1, 2, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 2, 1, 1, 2, 0, 1, 0, 0, 1, 1, 2, 1, 1, 1, 0, 1, 1, 1, 2, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 2, 1, 3, 0, 2, 2, 2, 1, 2, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 0, 2, 0, 1, 0, 0, 2, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 2, 0, 1, 2, 1, 0, 0, 0, 0, 1, 1, 1, 0, 2, 2, 2, 1, 1, 1, 0, 2, 2, 2, 1, 1, 1, 1, 0, 2, 0, 1, 1, 1, 0, 2, 1, 1, 0, 1, 1, 2, 1, 1, 1, 2, 2, 1, 0, 2, 1, 0, 1, 1, 0, 2, 0, 2, 2, 1, 1, 1, 0, 0, 0, 1, 2, 2, 2, 1, 0, 0, 0, 2, 2, 0, 0, 2, 0, 2, 1, 0, 0, 1, 1, 2, 2, 1, 1, 1, 2, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 3, 0, 1, 0, 0, 0, 1, 1, 0, 2, 1, 1, 0, 1, 2, 1, 0, 2, 0, 0, 2, 1, 2, 1, 1, 0, 1, 0, 1, 0, 1, 2, 0, 0, 0, 1, 2, 3, 0, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 0, 1, 1, 1, 1, 2, 1, 0, 1, 1, 2, 3, 0, 0, 1, 1, 3, 1, 2, 1, 0, 1, 0, 0, 1, 1, 3, 2, 2, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 2, 1, 0, 1, 2, 1, 0, 1, 0, 0, 2, 2, 1, 1, 1, 1, 1, 2, 2, 2, 2, 1, 0, 1, 1, 2, 0, 2, 0, 0, 4, 1, 0, 1, 2, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 2, 0, 1, 2, 0, 1, 2, 0, 2, 2, 0, 0, 3, 1, 1, 1, 1, 1, 1, 0, 0, 1, 2, 1, 1, 1, 1, 1, 2, 1, 0, 0, 3, 0, 2, 1, 0, 0, 2, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 2, 0, 0, 1, 2, 2, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 2, 2, 0, 0, 3, 1, 2, 2, 0, 1, 2, 2, 2, 1, 1, 0, 1, 3, 0, 0, 3, 1, 1, 0, 3, 1, 1, 2, 0, 1, 1, 1, 1, 3, 1, 2, 1, 1, 2, 2, 2, 0, 0, 1, 1, 0, 3, 1, 0, 2, 1, 0, 1, 1, 1, 0, 0, 2, 2, 1, 2, 1, 0, 1, 1, 1, 0, 2, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 3, 1, 1, 1, 1, 1, 0, 1, 1, 1, 3, 0, 2, 0, 2, 1, 0, 2, 1, 0, 0, 0, 1, 1, 2, 0, 1, 0, 2, 1, 1, 1, 2, 2, 1, 1, 0, 0, 0, 0, 1, 1, 2, 0, 1, 2, 1, 2, 1, 2, 1, 1, 1, 3, 0, 1, 0, 0, 2, 2, 0, 0, 0, 2, 2, 2, 1, 1, 2, 2, 1, 3, 1, 1, 0, 0, 2, 2, 0, 1, 0, 0, 2, 2, 1, 2, 1, 2, 1, 2, 2, 1, 1, 0, 2, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 2, 2, 2, 2, 2, 1, 1, 1, 0, 0, 2, 0, 1, 0, 1, 2, 1, 1, 2, 2, 2, 0, 0, 1, 0, 1, 1, 1, 0, 2, 1, 2, 1, 1, 1, 2, 1, 0, 1, 0, 2, 2, 1, 1, 1, 1, 0, 0, 0, 0, 2, 2, 1, 0, 2, 1, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 3, 1, 1, 0, 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 1, 1, 1, 0, 2, 0, 2, 0, 2, 2, 3, 1, 2, 0, 1, 1, 1, 2, 0, 0, 1, 1, 1, 0, 1, 2, 3, 1, 1, 2, 0, 1, 1, 1, 2, 2, 2, 2, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 2, 0, 2, 0, 2, 0, 2, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 3, 1, 2, 1, 1, 2, 1, 1, 0, 1, 2, 0, 1, 1, 2, 2, 0, 0, 0, 1, 1, 1, 2, 1, 1, 2, 2, 2, 1, 1, 1, 1, 0, 1, 1, 2, 0, 1, 1, 3, 2, 0, 0, 1, 2, 2, 2, 1, 2, 0, 2, 0, 0, 2, 0, 1, 1, 0, 1, 1, 2, 1, 0, 2, 1, 2, 2, 1, 1, 1, 0, 1, 1, 2, 0, 1, 2, 0, 1, 3, 0, 1, 1, 1, 0, 0, 1, 0, 1, 2, 0, 0, 2, 1, 0, 2, 1, 1, 3, 3, 0, 2, 2, 0, 2, 0, 1, 0, 0, 0, 1, 2, 0, 0, 2, 3, 0, 1, 2, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 2, 1, 1, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 0, 0, 0, 2, 2, 1, 1, 1, 1, 0, 1, 2, 0, 1, 1, 2, 1, 1, 1, 1, 0, 3, 2, 0, 0, 1, 2, 2, 0, 2, 0, 1, 0, 1, 1, 0, 0, 0, 1, 2, 1, 0, 1, 2, 1, 3, 1, 1, 1, 1, 1, 0, 1, 1, 2, 1, 1, 1, 0, 1, 1, 2, 0, 3, 2, 1, 0, 2, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 0, 1, 1, 2, 1, 0, 2, 4, 1, 0, 2, 0, 0, 0, 1, 2, 1, 0, 1, 0, 1, 2, 1, 2, 1, 0, 1, 1, 1, 2, 3, 0, 1, 2, 0, 1, 0, 1, 1, 0, 3, 1, 1, 2, 1, 1, 2, 0, 2, 1, 0, 1, 2, 2, 0, 1, 1, 1, 0, 0, 2, 1, 0, 2, 0, 0, 2, 0, 1, 1, 1, 1, 2, 0, 0, 0, 2, 2, 0, 0, 3, 1, 2, 0, 0, 2, 0, 3, 0, 0, 2, 1, 2, 0, 1, 0, 1, 1, 2, 0, 1, 1, 0, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 1, 0, 0, 1, 1, 0, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 2, 2, 2, 1, 0, 1, 0, 3, 2, 1, 0, 0, 2, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 3, 0, 1, 1, 2, 3, 0, 2, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 2, 0, 1, 0, 1, 0, 2, 1, 0, 2, 1, 0, 0, 1, 1, 0, 0, 2, 2, 1, 2, 2, 0, 1, 0, 1, 2, 1, 1, 1, 1, 3, 1, 0, 0, 1, 0, 1, 0, 0, 2, 2, 1, 1, 1, 0, 0, 1, 1, 1, 2, 2, 0, 1, 0, 0, 1, 0, 0, 2, 0, 1, 0, 2, 2, 2, 2, 1, 1, 2, 1, 1, 0, 1, 1, 2, 1, 3, 2, 1, 0, 3, 2, 2, 0, 2, 0, 0, 2, 1, 3, 1, 1, 1, 1, 1, 3, 3, 2, 2, 1, 0, 1, 1, 3, 1, 1, 0, 2, 2, 1, 0, 1, 1, 1, 1, 1, 1, 0, 2, 1, 0, 1, 1, 1, 2, 1, 0, 0, 1, 1, 1, 0, 1, 0, 2, 0, 1, 1, 2, 1, 0, 2, 0, 0, 0, 1, 2, 1, 2, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 2, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 2, 2, 4, 2, 1, 2, 1, 0, 2, 1, 0, 1, 1, 0, 0, 0, 0, 2, 3, 2, 1, 0, 1, 0, 2, 0, 0, 1, 3, 1, 0, 1, 0, 0, 1, 3, 2, 2, 1, 0, 1, 1, 2, 1, 0, 1, 1, 0, 2, 1, 0, 1, 1, 0, 0, 0, 0, 2, 1, 1, 0, 0, 1, 2, 1, 0, 0, 1, 2, 3, 1, 2, 1, 1, 2, 1, 1, 2, 2, 1, 2, 1, 0, 1, 3, 2, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 2, 1, 0, 1, 1, 1, 0, 1, 0, 0, 2, 2, 0, 1, 0, 1, 0, 0, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 2, 0, 0, 1, 2, 0, 1, 1, 1, 1, 0, 2, 1, 0, 0, 1, 3, 0, 2, 2, 1, 1, 1, 3, 3, 4, 0, 0, 1, 1, 1, 0, 1, 0, 0, 3, 2, 1, 0, 1, 0, 0, 0, 0, 0, 3, 2, 1, 0, 3, 0, 3, 1, 1, 1, 1, 1, 0, 2, 0, 2, 0, 2, 2, 1, 3, 2, 1, 1, 0, 2, 2, 2, 1, 3, 0, 0, 1, 2, 3, 0, 0, 1, 2, 0, 0, 0, 1, 0, 1, 2, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 2, 2, 0, 3, 1, 1, 2, 0, 2, 1, 2, 2, 1, 1, 2, 1, 0, 3, 3, 2, 0, 1, 0, 2, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 2, 2, 0, 1, 3, 1, 1, 2, 1, 0, 1, 0, 0, 2, 0, 1, 2, 2, 1, 1, 1, 0, 0, 3, 2, 2, 1, 0, 1, 1, 1, 2, 1, 0, 1, 1, 1, 1, 1, 0, 2, 2, 1, 0, 1, 3, 3, 1, 1, 0, 3, 0, 1, 1, 2, 0, 1, 2, 0, 0, 1, 1, 1, 1, 2, 1, 2, 3, 0, 1, 0, 0, 1, 1, 3, 1, 3, 1, 1, 0, 3, 1, 2, 0, 0, 1, 0, 1, 0, 2, 0, 0, 2, 0, 2, 1, 1, 0, 0, 0, 1, 1, 1, 1, 2, 0, 1, 2, 1, 2, 1, 2, 0, 1, 3, 1, 2, 0, 1, 1, 0, 0, 1, 1, 2, 2, 1, 1, 3, 2, 0, 2, 3, 1, 0, 2, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 2, 1, 0, 2, 1, 1, 2, 1, 1, 0, 1, 2, 2, 1, 1, 3, 3, 0, 0, 1, 0, 2, 0, 3, 0, 0, 1, 0, 2, 1, 1, 0, 1, 1, 0, 0, 1, 2, 1, 2, 1, 0, 0, 2, 1, 1, 2, 1, 2, 2, 0, 1, 1, 1, 2, 0, 2, 2, 0, 1, 0, 2, 0, 2, 1, 1, 1, 0, 2, 0, 0, 2, 1, 0, 0, 0, 2, 0, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 1, 0, 1, 1, 1, 3, 0, 0, 0, 1, 1, 1, 1, 1, 0, 2, 1, 1, 1, 0, 1, 1, 1, 1, 2, 0, 1, 0, 1, 0, 2, 1, 0, 1, 0, 0, 1, 0, 1, 0, 2, 1, 0, 2, 2, 2, 0, 0, 2, 2, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 2, 1, 2, 0, 0, 2, 2, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 2, 3, 1, 0, 0, 1, 1, 2, 0, 1, 2, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 2, 1, 2, 1, 1, 2, 2, 1, 1, 0, 1, 0, 3, 1, 1, 2, 0, 1, 0, 2, 1, 2, 1, 1, 3, 0, 3, 1, 2, 2, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 0, 1, 0, 2, 1, 2, 1, 1, 1, 2, 2, 0, 0, 1, 3, 3, 2, 1, 2, 0, 2, 1, 0, 0, 1, 2, 2, 1, 0, 2, 1, 1, 0, 3, 2, 2, 1, 0, 1, 2, 1, 0, 3, 2, 1, 2, 1, 1, 0, 2, 1, 3, 1, 2, 0, 1, 2, 3, 1, 1, 1, 1, 2, 0, 0, 0, 1, 0, 1, 1, 2, 2, 2, 0, 0, 1, 1, 1, 1, 1, 1, 0, 3, 2, 1, 0, 1, 1, 1, 0, 2, 0, 1, 2, 1, 2, 0, 0, 1, 2, 0, 1, 2, 0, 1, 0, 1, 2, 1, 2, 1, 0, 1, 1, 0, 1, 3, 1, 1, 1, 1, 1, 1, 1, 3, 0, 1, 2, 0, 2, 2, 1, 1, 0, 2, 1, 2, 1, 1, 3, 0, 0, 1, 1, 2, 2, 3, 1, 1, 1, 0, 0, 1, 0, 0, 1, 2, 0, 0, 0, 0, 1, 0, 3, 3, 0, 1, 1, 0, 1, 1, 1, 3, 1, 1, 1, 0, 1, 2, 1, 0, 2, 1, 1, 1, 2, 1, 3, 0, 0, 3, 1, 1, 0, 1, 1, 0, 2, 3, 2, 1, 2, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 2, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 2, 0, 1, 2, 1, 3, 0, 2, 2, 1, 2, 1, 1, 1, 2, 2, 2, 1, 2, 1, 1, 1, 1, 0, 0, 1, 2, 1, 2, 2, 1, 0, 1, 2, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 2, 1, 0, 1, 0, 0, 1, 1, 0, 2, 1, 2, 2, 2, 1, 1, 2, 1, 1, 1, 2, 1, 2, 0, 1, 3, 1, 1, 3, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 2, 1, 2, 2, 2, 1, 1, 1, 0, 2, 0, 1, 1, 0, 0, 1, 2, 1, 2, 1, 3, 1, 2, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 2, 0, 1, 2, 1, 2, 3, 0, 0, 2, 1, 1, 0, 0, 2, 1, 1, 1, 2, 1, 0, 2, 1, 3, 3, 2, 1, 0, 0, 0, 1, 1, 1, 0, 2, 1, 0, 1, 1, 2, 1, 1, 2, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 2, 0, 1, 0, 2, 2, 0, 1, 0, 0, 1, 1, 0, 2, 1, 1, 1, 1, 0, 2, 2, 1, 1, 0, 3, 0, 1, 1, 1, 0, 2, 2, 1, 2, 1, 1, 0, 3, 2, 1, 1, 2, 3, 2, 3, 1, 2, 0, 3, 1, 1, 2, 2, 0, 0, 2, 0, 2, 1, 0, 2, 1, 1, 1, 0, 2, 0, 1, 0, 1, 1, 0, 2, 0, 1, 3, 0, 1, 2, 0, 2, 0, 0, 0, 1, 2, 2, 2, 1, 2, 1, 1, 0, 0, 0, 1, 1, 0, 2, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 3, 2, 1, 1, 2, 0, 2, 4, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 2, 2, 1, 1, 1, 3, 0, 3, 1, 2, 2, 2, 0, 1, 0, 2, 1, 1, 1, 2, 2, 0, 2, 3, 2, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 2, 1, 0, 1, 0, 1, 1, 2, 0, 1, 0, 1, 2, 1, 3, 0, 1, 1, 1, 2, 2, 2, 0, 1, 2, 2, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 2, 2, 0, 1, 1, 1, 1, 2, 1, 0, 0, 1, 0, 3, 0, 2, 1, 0, 1, 1, 0, 2, 1, 0, 3, 1, 0, 0, 2, 0, 0, 2, 3, 1, 0, 0, 0, 0, 1, 0, 1, 2, 2, 1, 0, 1, 0, 0, 0, 0, 2, 0, 0, 2, 2, 2, 1, 1, 0, 2, 2, 2, 0, 1, 1, 2, 2, 0, 0, 0, 2, 1, 0, 1, 0, 1, 1, 2, 1, 1, 2, 2, 1, 2, 0, 3, 0, 1, 0, 2, 1, 0, 1, 1, 1, 3, 1, 1, 0, 1, 2, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 3, 0, 0, 0, 2, 2, 2, 1, 0, 0, 0, 3, 1, 0, 0, 1, 0, 1, 2, 3, 1, 1, 0, 2, 1, 1, 1, 1, 3, 0, 1, 1, 1, 0, 2, 2, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 2, 0, 1, 1, 1, 2, 0, 1, 1, 1, 1, 2, 0, 1, 0, 1, 2, 2, 0, 3, 1, 1, 3, 3, 2, 2, 0, 2, 0, 1, 0, 2, 2, 2, 1, 1, 0, 1, 2, 1, 1, 1, 3, 1, 1, 1, 2, 0, 1, 0, 1, 0, 2, 2, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 3, 1, 0, 0, 3, 1, 2, 0, 2, 3, 2, 1, 0, 0, 2, 0, 0, 2, 2, 0, 0, 0, 3, 1, 3, 0, 0, 0, 1, 0, 2, 0, 0, 1, 1, 1, 1, 1, 2, 2, 0, 1, 1, 3, 0, 2, 0, 1, 1, 1, 1, 1, 1, 2, 1, 0, 2, 1, 1, 2, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 2, 2, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 3, 1, 3, 2, 2, 2, 1, 1, 2, 2, 2, 1, 0, 0, 1, 0, 2, 0, 0, 1, 1, 0, 1, 0, 1, 2, 0, 1, 1, 0, 1, 0, 2, 1, 1, 2, 3, 2, 1, 1, 2, 1, 1, 0, 0, 0, 1, 1, 2, 2, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 2, 2, 3, 1, 0, 1, 2, 1, 1, 1, 1, 2, 3, 0, 1, 1, 1, 2, 0, 1, 0, 1, 2, 0, 2, 1, 2, 0, 0, 1, 3, 0, 1, 1, 1, 2, 3, 1, 1, 2, 0, 1, 0, 2, 0, 2, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 2, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 3, 1, 0, 3, 0, 0, 0, 1, 2, 1, 0, 2, 1, 0, 1, 2, 1, 1, 1, 0, 1, 0, 1, 0, 3, 1, 1, 0, 1, 1, 2, 0, 2, 0, 2, 2, 1, 2, 1, 1, 0, 2, 1, 0, 0, 1, 0, 1, 2, 0, 1, 1, 0, 0, 0, 2, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 3, 0, 1, 0, 0, 2, 1, 2, 0, 1, 1, 2, 1, 0, 3, 1, 1, 1, 3, 1, 2, 0, 1, 1, 2, 2, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 2, 1, 3, 2, 1, 0, 1, 3, 2, 1, 1, 2, 0, 1, 1, 1, 1, 0, 0, 1, 2, 3, 2, 0, 1, 1, 1, 1, 0, 2, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 2, 0, 1, 1, 3, 2, 1, 0, 2, 1, 1, 2, 2, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 2, 1, 0, 2, 1, 0, 0, 1, 2, 0, 1, 0, 1, 0, 1, 2, 1, 2, 0, 1, 1, 1, 1, 1, 2, 0, 0, 0, 1, 0, 2, 1, 2, 0, 2, 1, 1, 0, 2, 2, 3, 2, 0, 2, 0, 1, 0, 1, 0, 2, 0, 1, 2, 1, 2, 2, 0, 1, 2, 0, 1, 2, 0, 2, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 2, 1, 0, 0, 3, 0, 1, 0, 2, 1, 0, 1, 1, 3, 3, 1, 0, 0, 0, 3, 1, 4, 1, 0, 0, 0, 1, 1, 0, 1, 1, 2, 0, 1, 1, 0, 0, 0, 0, 2, 2, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 0, 1, 3, 2, 1, 1, 1, 0, 2, 1, 0, 0, 0, 0, 1, 0, 1, 0, 2, 1, 0, 1, 0, 3, 1, 0, 1, 1, 0, 2, 2, 1, 1, 0, 0, 1, 0, 1, 2, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 2, 1, 1, 3, 1, 2, 1, 0, 3, 0, 2, 0, 1, 1, 1, 2, 1, 2, 1, 2, 1, 0, 0, 2, 0, 1, 3, 2, 0, 2, 1, 1, 1, 0, 0, 3, 1, 2, 0, 1, 1, 1, 0, 0, 1, 0, 1, 2, 1, 1, 1, 0, 1, 0, 2, 1, 2, 2, 0, 2, 1, 1, 1, 3, 1, 0, 1, 0, 1, 1, 1, 1, 4, 1, 1, 0, 2, 2, 2, 1, 0, 1, 1, 1, 0, 2, 1, 0, 0, 2, 0, 1, 0, 0, 0, 1, 1, 0, 2, 1, 1, 0, 3, 0, 0, 0, 1, 2, 2, 1, 0, 1, 1, 2, 2, 1, 1, 2, 1, 0, 2, 1, 1, 0, 3, 4, 0, 1, 1, 0, 1, 2, 1, 2, 2, 2, 0, 1, 2, 1, 0, 1, 0, 1, 2, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 0, 2, 0, 1, 1, 0, 1, 1, 1, 4, 1, 2, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1, 1, 2, 0, 0, 1, 3, 2, 2, 3, 0, 1, 1, 1, 1, 1, 2, 2, 1, 1, 0, 0, 1, 1, 2, 0, 1, 2, 2, 1, 1, 3, 0, 0, 1, 1, 2, 2, 1, 2, 2, 2, 0, 3, 0, 2, 2, 0, 1, 0, 1, 0, 1, 1, 1, 2, 0, 1, 2, 2, 0, 0, 0, 1, 1, 2, 3, 3, 0, 1, 3, 0, 1, 2, 1, 1, 2, 1, 0, 1, 2, 1, 0, 0, 0, 1, 2, 1, 1, 1, 0, 1, 3, 2, 0, 0, 2, 0, 1, 1, 1, 0, 1, 1, 1, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 0, 0, 3, 0, 0, 2, 1, 2, 0, 0, 0, 3, 0, 2, 1, 3, 2, 1, 1, 1, 0, 1, 2, 1, 0, 1, 0, 1, 2, 2, 1, 0, 1, 1, 1, 3, 0, 0, 0, 1, 1, 0, 3, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 2, 1, 0, 3, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 2, 2, 1, 1, 0, 2, 2, 0, 2, 0, 2, 1, 2, 2, 2, 0, 0, 1, 0, 1, 2, 1, 2, 1, 1, 0, 2, 0, 0, 1, 2, 1, 0, 0, 1, 1, 2, 1, 1, 1, 2, 1, 2, 2, 1, 2, 1, 0, 0, 2, 2, 2, 2, 1, 1, 0, 2, 0, 1, 2, 0, 2, 1, 2, 2, 0, 0, 1, 1, 1, 2, 1, 0, 2, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 2, 2, 1, 1, 0, 1, 1, 2, 1, 0, 3, 1, 2, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 2, 0, 1, 1, 2, 3, 1, 1, 1, 0, 0, 1, 0, 1, 2, 2, 2, 1, 2, 0, 0, 0, 0, 1, 2, 0, 1, 0, 0, 0, 2, 0, 2, 1, 2, 2, 1, 1, 1, 1, 0, 0, 1, 1, 2, 1, 3, 3, 1, 1, 1, 1, 0, 1, 1, 1, 0, 2, 1, 1, 1, 2, 1, 0, 1, 0, 0, 0, 0, 2, 1, 1, 1, 1, 2, 1, 0, 2, 1, 0, 0, 1, 1, 1, 1, 0, 2, 0, 0, 0, 0, 1, 1, 2, 2, 0, 0, 1, 2, 0, 1, 0, 2, 1, 3, 1, 0, 1, 1, 0, 1, 0, 2, 2, 2, 0, 1, 0, 2, 1, 0, 1, 1, 2, 1, 0, 1, 1, 1, 1, 2, 3, 0, 0, 1, 1, 1, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 1, 2, 0, 1, 1, 1, 2, 1, 0, 0, 1, 1, 2, 1, 2, 2, 1, 1, 0, 2, 1, 1, 1, 1, 1, 0, 2, 1, 1, 1, 1, 1, 0, 1, 1, 2, 0, 1, 1, 1, 0, 1, 2, 1, 1, 0, 1, 2, 1, 0, 1, 2, 1, 1, 0, 0, 2, 2, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 2, 0, 2, 1, 0, 1, 0, 3, 2, 1, 2, 0, 2, 2, 2, 0, 0, 1, 0, 1, 1, 1, 1, 1, 3, 2, 0, 1, 0, 1, 3, 1, 2, 0, 2, 0, 1, 2, 2, 0, 1, 3, 1, 2, 0, 2, 0, 1, 2, 1, 2, 1, 1, 1, 1, 1, 0, 2, 0, 1, 1, 0, 2, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 2, 2, 1, 1, 1, 1, 0, 1, 1, 2, 2, 1, 1, 1, 2, 0, 0, 3, 1, 1, 3, 1, 1, 1, 2, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 2, 0, 1, 1, 1, 1, 1, 1, 0, 2, 0, 0, 1, 0, 1, 1, 2, 0, 1, 1, 2, 1, 2, 0, 0, 1, 0, 1, 0, 0, 2, 1, 2, 0, 1, 0, 0, 2, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 2, 0, 0, 0, 2, 2, 2, 0, 1, 2, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 0, 2, 1, 1, 1, 0, 1, 0, 1, 3, 0, 1, 1, 0, 1, 2, 2, 1, 3, 2, 1, 0, 0, 0, 1, 0, 3, 1, 1, 3, 1, 2, 2, 1, 0, 1, 1, 2, 3, 1, 0, 2, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 2, 0, 0, 0, 0, 1, 3, 0, 2, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 3, 2, 0, 3, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 0, 1, 0, 0, 0, 1, 0, 2, 0, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 0, 3, 2, 2, 2, 1, 0, 1, 1, 1, 2, 0, 2, 1, 2, 2, 1, 1, 2, 0, 1, 0, 3, 0, 1, 2, 0, 1, 2, 1, 0, 0, 0, 1, 2, 1, 1, 0, 1, 1, 0, 2, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 2, 1, 1, 1, 0, 0, 0, 2, 0, 0, 0, 0, 2, 1, 1, 2, 0, 3, 0, 1, 0, 1, 1, 2, 1, 1, 1, 1, 1, 0, 1, 2, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 3, 0, 2, 0, 0, 1, 1, 0, 2, 0, 3, 2, 1, 2, 0, 1, 2, 1, 0, 1, 1, 1, 2, 1, 1, 1, 2, 1, 0, 1, 0, 1, 1, 0, 1, 1, 2, 1, 1, 0, 2, 0, 1, 1, 1, 2, 1, 0, 0, 2, 0, 0, 1, 1, 1, 2, 2, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 3, 1, 0, 0, 2, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 2, 0, 1, 2, 0, 2, 1, 1, 1, 1, 3, 0, 0, 1, 2, 1, 2, 1, 1, 0, 1, 0, 1, 0, 2, 1, 1, 2, 0, 1, 1, 1, 1, 1, 0, 2, 1, 2, 1, 2, 1, 2, 0, 1, 1, 0, 0, 1, 2, 0, 1, 2, 0, 1, 0, 0, 2, 2, 1, 2, 1, 1, 1, 0, 1, 1, 0, 2, 0, 1, 0, 1, 0, 2, 1, 1, 0, 3, 1, 0, 1, 1, 0, 0, 1, 0, 2, 1, 0, 1, 1, 1, 1, 1, 0, 3, 1, 0, 2, 2, 1, 0, 0, 1, 0, 2, 1, 1, 0, 1, 2, 0, 1, 0, 1, 1, 0, 1, 0, 2, 0, 1, 1, 0, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2, 1, 2, 1, 1, 2, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 2, 0, 0, 0, 2, 2, 2, 0, 2, 1, 1, 1, 1, 1, 0, 1, 1, 2, 0, 2, 0, 1, 2, 1, 0, 2, 1, 1, 1, 1, 2, 2, 0, 1, 2, 1, 1, 1, 0, 2, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 2, 0, 1, 1, 2, 2, 2, 0, 1, 0, 2, 1, 0, 2, 3, 1, 1, 2, 0, 2, 1, 2, 1, 0, 1, 2, 1, 0, 0, 1, 1, 2, 2, 1, 1, 0, 1, 0, 3, 2, 1, 2, 1, 1, 2, 0, 1, 1, 0, 0, 2, 0, 2, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 2, 0, 1, 1, 1, 1, 1, 1, 1, 2, 0, 1, 1, 2, 1, 0, 1, 0, 1, 3, 1, 0, 2, 1, 1, 0, 0, 2, 2, 1, 1, 1, 0, 0, 1, 2, 0, 2, 0, 2, 0, 0, 1, 0, 2, 2, 2, 1, 2, 0, 0, 1, 1, 2, 0, 1, 2, 1, 2, 1, 3, 1, 0, 1, 1, 2, 1, 2, 0, 1, 2, 2, 1, 1, 1, 0, 2, 2, 2, 1, 0, 1, 2, 2, 1, 2, 3, 2, 2, 1, 1, 0, 3, 2, 0, 1, 1, 0, 1, 2, 2, 1, 2, 0, 1, 1, 0, 0, 2, 2, 2, 1, 2, 0, 0, 1, 2, 1, 1, 1, 0, 2, 0, 1, 1, 1, 2, 0, 1, 1, 1, 1, 0, 3, 1, 3, 2, 0, 2, 2, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 2, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 2, 2, 0, 2, 4, 1, 2, 0, 1, 0, 1, 1, 1, 0, 2, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 2, 0, 3, 0, 1, 1, 2, 1, 1, 1, 1, 2, 0, 0, 1, 1, 2, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 2, 1, 1, 0, 2, 0, 1, 1, 1, 2, 2, 3, 1, 1, 1, 1, 1, 3, 1, 1, 2, 1, 2, 2, 1, 1, 2, 0, 0, 1, 2, 0, 0, 2, 2, 1, 1, 2, 0, 0, 2, 2, 1, 0, 1, 1, 1, 1, 0, 2, 2, 0, 1, 1, 2, 1, 0, 2, 1, 2, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 2, 1, 1, 1, 2, 1, 0, 1, 1, 1, 1, 1, 0, 2, 0, 2, 2, 1, 2, 1, 2, 1, 1, 1, 3, 2, 0, 0, 2, 1, 2, 1, 1, 1, 1, 0, 1, 1, 2, 0, 2, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 4, 2, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 2, 1, 3, 1, 0, 0, 0, 1, 2, 2, 0, 0, 2, 1, 4, 2, 0, 2, 1, 0, 2, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 2, 1, 1, 1, 0, 0, 0, 0, 1, 0, 3, 0, 1, 3, 3, 0, 2, 1, 0, 2, 1, 2, 0, 1, 1, 1, 2, 1, 0, 1, 0, 1, 3, 1, 1, 1, 0, 1, 1, 0, 0, 1, 2, 1, 0, 0, 1, 0, 1, 3, 1, 2, 2, 0, 0, 2, 1, 1, 2, 2, 1, 2, 1, 1, 0, 0, 0, 1, 0, 1, 0, 2, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 2, 0, 0, 0, 2, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 2, 2, 2, 1, 0, 0, 1, 2, 0, 1, 1, 2, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 2, 2, 0, 0, 0, 0, 0, 1, 1, 0, 2, 2, 2, 1, 1, 2, 2, 3, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 0, 3, 1, 0, 2, 1, 1, 1, 3, 3, 2, 0, 0, 1, 1, 1, 0, 1, 1, 2, 0, 1, 1, 0, 0, 1, 2, 2, 0, 2, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 2, 2, 1, 2, 1, 2, 0, 2, 1, 0, 2, 0, 1, 1, 1, 1, 2, 3, 2, 0, 1, 1, 0, 0, 2, 2, 1, 1, 1, 1, 2, 3, 0, 2, 0, 1, 1, 2, 0, 2, 1, 0, 1, 1, 1, 1, 1, 1, 2, 1, 2, 3, 0, 2, 1, 1, 1, 1, 1, 2, 1, 2, 2, 1, 1, 0, 0, 0, 2, 1, 0, 2, 0, 0, 2, 0, 1, 1, 1, 2, 2, 2, 2, 2, 1, 0, 3, 2, 0, 0, 1, 3, 1, 1, 0, 1, 2, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 2, 1, 0, 2, 0, 2, 2, 1, 0, 0, 2, 0, 0, 1, 1, 1, 1, 3, 0, 0, 0, 1, 1, 1, 2, 0, 1, 1, 0, 2, 2, 1, 0, 1, 1, 2, 2, 3, 2, 0, 0, 4, 1, 0, 2, 0, 2, 1, 2, 0, 0, 2, 1, 1, 1, 1, 1, 3, 0, 1, 0, 2, 2, 2, 1, 3, 1, 0, 2, 3, 1, 0, 0, 0, 3, 0, 2, 3, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 1, 0, 1, 1, 0, 2, 0, 1, 1, 0, 2, 1, 0, 1, 1, 0, 1, 0, 1, 2, 1, 0, 1, 1, 0, 3, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 2, 0, 2, 1, 1, 1, 0, 1, 1, 2, 1, 2, 1, 2, 1, 2, 2, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 2, 0, 1, 1, 2, 1, 2, 1, 1, 0, 2, 1, 1, 1, 1, 1, 1, 0, 1, 1, 2, 3, 2, 0, 1, 1, 0, 1, 0, 1, 1, 0, 2, 1, 0, 2, 1, 1, 1, 0, 1, 2, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 2, 1, 1, 0, 1, 0, 1, 3, 1, 1, 0, 1, 1, 0, 1, 1, 3, 0, 0, 1, 3, 2, 1, 2, 1, 0, 2, 0, 1, 1, 0, 2, 2, 1, 1, 3, 2, 1, 1, 0, 2, 2, 2, 1, 1, 1, 0, 1, 0, 1, 2, 1, 0, 0, 0, 1, 1, 1, 2, 1, 0, 2, 1, 1, 1, 0, 0, 0, 1, 2, 0, 2, 0, 0, 2, 2, 0, 1, 2, 1, 0, 0, 0, 0, 0, 0, 2, 1, 1, 2, 1, 0, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 3, 1, 2, 0, 1, 0, 1, 1, 2, 0, 0, 0, 0, 0, 0, 2, 0, 1, 0, 2, 1, 0, 2, 2, 1, 0, 0, 2, 0, 4, 1, 3, 0, 0, 1, 1, 0, 1, 2, 1, 1, 1, 2, 1, 0, 1, 0, 0, 2, 0, 0, 2, 1, 1, 2, 1, 2, 0, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 0, 1, 1, 1, 0, 1, 2, 1, 2, 1, 2, 2, 1, 1, 1, 0, 1, 2, 2, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 2, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 2, 1, 1, 1, 1, 0, 0, 2, 0, 0, 0, 0, 1, 0, 1, 3, 1, 3, 1, 0, 1, 1, 2, 2, 2, 0, 0, 2, 0, 1, 1, 2, 1, 1, 0, 1, 2, 0, 1, 0, 1, 0, 0, 1, 2, 2, 1, 1, 2, 0, 1, 0, 2, 2, 2, 2, 0, 0, 1, 2, 1, 2, 2, 1, 1, 1, 2, 1, 1, 0, 0, 2, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 3, 1, 0, 1, 0, 1, 0, 2, 1, 0, 0, 0, 3, 2, 1, 0, 3, 2, 0, 1, 1, 1, 1, 0, 1, 1, 1, 2, 1, 1, 0, 0, 2, 1, 0, 1, 1, 0, 1, 2, 1, 0, 0, 1, 0, 1, 0, 3, 1, 0, 0, 0, 1, 1, 0, 2, 1, 1, 1, 0, 1, 2, 0, 2, 1, 2, 1, 2, 0, 0, 1, 0, 2, 1, 2, 2, 2, 2, 0, 1, 1, 2, 0, 2, 0, 1, 1, 0, 0, 1, 1, 1, 2, 3, 1, 1, 3, 1, 3, 1, 1, 3, 1, 0, 2, 1, 2, 2, 1, 0, 0, 2, 1, 1, 0, 0, 0, 0, 1, 0, 3, 1, 1, 1, 2, 2, 1, 0, 0, 0, 1, 1, 1, 3, 2, 1, 0, 1, 0, 1, 2, 0, 1, 0, 0, 0, 1, 0, 3, 0, 2, 0, 1, 0, 2, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0, 2, 1, 2, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 0, 2, 0, 1, 1, 0, 0, 0, 1, 2, 0, 0, 0, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 2, 0, 2, 1, 2, 1, 1, 2, 0, 1, 3, 0, 0, 1, 1, 1, 1, 0, 0, 0, 2, 2, 1, 1, 1, 3, 1, 2, 0, 2, 1, 1, 0, 3, 1, 1, 1, 0, 0, 1, 0, 2, 1, 2, 1, 1, 0, 1, 2, 1, 1, 2, 4, 1, 2, 2, 1, 1, 1, 2, 2, 1, 3, 0, 2, 1, 1, 2, 2, 2, 1, 1, 2, 1, 2, 2, 1, 1, 3, 1, 2, 0, 1, 2, 1, 0, 0, 3, 1, 0, 0, 1, 0, 0, 2, 2, 2, 1, 2, 1, 2, 1, 2, 1, 0, 2, 0, 2, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 2, 0, 2, 2, 2, 1, 2, 1, 1, 0, 2, 1, 0, 1, 1, 0, 1, 1, 2, 2, 2, 2, 1, 1, 3, 2, 0, 0, 1, 1, 0, 3, 1, 1, 0, 1, 3, 1, 1, 1, 2, 0, 2, 2, 2, 1, 2, 0, 1, 2, 0, 1, 2, 0, 0, 0, 1, 0, 1, 3, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 2, 1, 2, 1, 3, 0, 2, 1, 0, 3, 1, 2, 3, 2, 1, 1, 1, 0, 1, 2, 1, 1, 0, 3, 2, 0, 1, 2, 0, 2, 0, 2, 1, 2, 1, 1, 1, 1, 1, 1, 0, 3, 1, 2, 0, 0, 3, 1, 0, 0, 1, 0, 0, 1, 0, 3, 0, 0, 2, 3, 1, 1, 0, 2, 1, 0, 1, 0, 0, 1, 1, 1, 0, 3, 0, 1, 0, 2, 0, 2, 1, 1, 1, 3, 1, 0, 1, 1, 1, 0, 1, 0, 1, 3, 1, 1, 2, 0, 2, 2, 2, 2, 0, 0, 1, 1, 2, 0, 1, 0, 2, 2, 2, 1, 0, 0, 0, 1, 1, 2, 1, 1, 2, 1, 1, 1, 2, 1, 1, 1, 0, 0, 3, 0, 1, 0, 1, 2, 1, 1, 1, 2, 1, 1, 0, 1, 1, 0, 1, 1, 2, 0, 1, 1, 1, 1, 1, 2, 0, 0, 2, 2, 2, 1, 0, 3, 3, 1, 1, 1, 2, 0, 1, 2, 1, 0, 0, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 0, 1, 0, 1, 2, 0, 2, 1, 2, 0, 0, 1, 1, 1, 1, 2, 1, 0, 0, 0, 2, 2, 2, 3, 2, 1, 2, 2, 1, 3, 0, 0, 3, 2, 1, 0, 1, 1, 0, 3, 1, 0, 2, 2, 2, 1, 1, 1, 1, 1, 1, 3, 0, 1, 2, 0, 1, 2, 1, 1, 2, 2, 1, 1, 1, 0, 2, 1, 2, 1, 0, 3, 0, 1, 1, 1, 1, 2, 2, 2, 1, 1, 3, 1, 1, 3, 0, 0, 2, 1, 1, 1, 1, 1, 1, 0, 1, 1, 2, 0, 1, 1, 1, 0, 1, 0, 0, 1, 2, 1, 0, 1, 0, 1, 2, 1, 3, 2, 1, 1, 0, 0, 3, 1, 0, 2, 1, 0, 1, 1, 0, 0, 1, 3, 2, 2, 2, 1, 0, 0, 0, 3, 0, 1, 1, 2, 0, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 2, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 3, 1, 2, 0, 1, 0, 0, 3, 1, 1, 0, 1, 1, 2, 0, 1, 2, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 2, 2, 1, 2, 1, 0, 3, 2, 1, 1, 0, 0, 1, 4, 1, 0, 1, 2, 0, 1, 3, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 2, 0, 0, 3, 0, 1, 2, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 2, 1, 0, 1, 2, 0, 0, 0, 2, 2, 0, 1, 1, 1, 1, 1, 1, 2, 0, 2, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 2, 1, 0, 1, 1, 2, 0, 1, 3, 1, 2, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1, 2, 3, 2, 1, 1, 3, 1, 1, 1, 2, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 2, 0, 1, 1, 0, 0, 1, 0, 1, 3, 1, 0, 0, 1, 0, 1, 1, 1, 2, 2, 2, 1, 0, 2, 3, 3, 1, 1, 1, 0, 2, 2, 1, 0, 1, 1, 1, 1, 0, 2, 3, 0, 2, 0, 2, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1, 1, 0, 3, 0, 1, 1, 0, 2, 1, 1, 1, 1, 0, 1, 0, 2, 2, 1, 1, 0, 0, 1, 0, 0, 0, 1, 2, 2, 1, 1, 1, 2, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 3, 1, 0, 3, 0, 1, 2, 0, 2, 1, 0, 0, 0, 3, 0, 2, 2, 0, 0, 2, 1, 0, 2, 2, 2, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 3, 0, 2, 2, 1, 0, 0, 0, 0, 2, 3, 1, 1, 1, 1, 1, 0, 0, 2, 3, 0, 0, 0, 1, 2, 0, 1, 1, 2, 1, 4, 3, 0, 2, 1, 1, 0, 1, 2, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 1, 3, 2, 1, 3, 1, 1, 1, 1, 1, 2, 0, 0, 0, 2, 0, 1, 1, 0, 1, 2, 2, 1, 3, 0, 1, 2, 0, 0, 1, 1, 1, 0, 2, 3, 1, 2, 1, 0, 3, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 2, 0, 0, 3, 1, 2, 1, 0, 0, 1, 1, 1, 1, 1, 2, 1, 1, 1, 3, 2, 1, 2, 0, 0, 1, 2, 2, 1, 1, 0, 2, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 2, 1, 1, 2, 1, 2, 1, 0, 1, 2, 1, 0, 3, 1, 0, 0, 1, 1, 1, 0, 0, 0, 3, 0, 1, 1, 3, 2, 1, 2, 1, 1, 0, 2, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 2, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 3, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 2, 3, 1, 0, 1, 2, 1, 1, 1, 0, 0, 0, 2, 1, 3, 1, 0, 0, 1, 1, 2, 1, 1, 2, 0, 1, 0, 1, 0, 0, 2, 0, 1, 2, 0, 3, 2, 0, 0, 1, 2, 1, 2, 0, 2, 1, 0, 3, 0, 1, 0, 2, 1, 0, 1, 1, 1, 2, 2, 2, 2, 1, 1, 1, 2, 2, 2, 2, 2, 2, 1, 3, 2, 1, 1, 2, 2, 2, 0, 0, 1, 1, 1, 2, 0, 0, 0, 2, 1, 0, 1, 1, 2, 2, 0, 2, 0, 2, 0, 2, 0, 0, 1, 1, 3, 1, 0, 0, 0, 0, 2, 0, 2, 1, 0, 2, 1, 0, 3, 1, 0, 1, 0, 1, 1, 0, 3, 2, 1, 0, 1, 1, 3, 2, 2, 2, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 2, 0, 2, 1, 0, 1, 2, 1, 0, 1, 0, 2, 2, 0, 1, 1, 2, 3, 0, 2, 1, 1, 0, 0, 1, 1, 2, 1, 1, 2, 0, 2, 2, 2, 0, 0, 1, 0, 1, 1, 2, 2, 1, 2, 1, 1, 1, 0, 1, 1, 2, 3, 0, 3, 1, 1, 0, 1, 1, 2, 1, 1, 0, 0, 0, 2, 2, 1, 1, 0, 1, 2, 1, 1, 0, 0, 1, 2, 1, 1, 0, 1, 1, 0, 0, 4, 1, 2, 0, 0, 3, 2, 1, 2, 0, 1, 1, 2, 1, 1, 1, 2, 0, 2, 1, 0, 2, 0, 0, 1, 3, 3, 0, 0, 1, 1, 1, 1, 2, 0, 1, 0, 1, 0, 1, 1, 3, 0, 2, 1, 1, 0, 0, 2, 2, 2, 0, 0, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 1, 1, 2, 0, 1, 0, 0, 0, 1, 1, 2, 1, 1, 1, 1, 2, 1, 3, 0, 1, 1, 3, 3, 1, 2, 3, 2, 1, 0, 2, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 2, 2, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 1, 0, 1, 1, 1, 1, 0, 0, 2, 0, 0, 0, 3, 0, 1, 1, 1, 0, 1, 1, 2, 1, 0, 0, 0, 1, 1, 1, 2, 2, 0, 2, 0, 1, 2, 2, 0, 2, 1, 2, 0, 2, 1, 0, 2, 1, 1, 0, 1, 2, 2, 1, 1, 0, 0, 0, 0, 2, 2, 0, 0, 1, 3, 1, 1, 0, 0, 2, 0, 1, 1, 2, 0, 2, 1, 0, 1, 3, 0, 2, 1, 0, 1, 1, 0, 1, 1, 3, 0, 2, 1, 1, 1, 0, 2, 2, 3, 1, 2, 1, 0, 1, 1, 1, 2, 2, 1, 2, 1, 0, 0, 1, 2, 2, 2, 0, 0, 1, 1, 0, 2, 1, 1, 1, 2, 0, 3, 1, 0, 2, 2, 2, 1, 2, 1, 1, 0, 2, 1, 2, 0, 2, 2, 0, 0, 2, 1, 1, 2, 2, 2, 2, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 3, 1, 2, 0, 0, 0, 1, 1, 0, 0, 2, 2, 1, 2, 2, 1, 0, 2, 0, 0, 0, 1, 0, 2, 1, 0, 1, 1, 1, 1, 3, 2, 0, 0, 1, 2, 2, 2, 4, 2, 0, 1, 1, 2, 1, 2, 1, 1, 2, 1, 2, 0, 3, 0, 2, 0, 3, 2, 1, 3, 2, 0, 3, 2, 2, 0, 1, 0, 1, 2, 1, 2, 1, 2, 2, 0, 1, 0, 1, 1, 0, 3, 2, 0, 1, 1, 2, 1, 2, 0, 2, 1, 1, 0, 1, 1, 1, 2, 1, 0, 0, 2, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 3, 0, 1, 0, 2, 1, 0, 1, 2, 2, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 2, 1, 0, 1, 0, 2, 2, 1, 1, 1, 0, 0, 1, 0, 2, 1, 1, 0, 1, 0, 1, 2, 1, 0, 1, 0, 1, 0, 1, 1, 2, 2, 0, 0, 0, 2, 2, 0, 1, 1, 1, 0, 1, 1, 1, 3, 1, 1, 2, 0, 0, 1, 0, 0, 2, 1, 1, 1, 1, 1, 1, 2, 2, 0, 1, 2, 0, 2, 1, 2, 2, 2, 0, 0, 1, 1, 4, 0, 1, 1, 2, 3, 0, 0, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 1, 0, 1, 0, 2, 2, 3, 3, 0, 2, 0, 0, 1, 0, 2, 1, 1, 2, 1, 2, 0, 0, 1, 1, 1, 1, 4, 2, 2, 2, 0, 2, 1, 1, 1, 0, 2, 2, 1, 1, 1, 2, 0, 1, 1, 0, 2, 0, 1, 1, 0, 1, 1, 2, 1, 1, 2, 0, 3, 1, 2, 1, 2, 0, 0, 1, 1, 1, 1, 1, 2, 0, 1, 1, 0, 1, 2, 3, 0, 3, 0, 0, 1, 1, 2, 1, 0, 1, 2, 1, 1, 0, 3, 3, 1, 1, 1, 1, 0, 1, 2, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0, 1, 2, 1, 2, 0, 2, 1, 1, 0, 1, 0, 0, 3, 1, 1, 1, 3, 2, 1, 1, 2, 1, 2, 1, 1, 1, 0, 1, 1, 2, 1, 1, 1, 2, 2, 2, 2, 0, 2, 1, 1, 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 1, 1, 2, 2, 1, 2, 0, 1, 1, 1, 2, 0, 1, 1, 2, 2, 1, 1, 0, 1, 1, 0, 0, 0, 2, 0, 1, 1, 1, 0, 1, 0, 0, 3, 2, 2, 2, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 3, 0, 0, 2, 1, 1, 2, 1, 1, 2, 0, 0, 1, 2, 0, 2, 0, 2, 0, 1, 1, 2, 3, 2, 1, 1, 0, 2, 1, 1, 0, 0, 2, 2, 0, 1, 1, 2, 1, 2, 1, 2, 1, 0, 2, 0, 1, 0, 3, 1, 1, 3, 2, 0, 1, 1, 0, 2, 1, 0, 2, 0, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 0, 1, 0, 2, 1, 2, 2, 1, 1, 2, 1, 0, 0, 0, 1, 3, 1, 0, 1, 2, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 2, 0, 3, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 2, 0, 1, 0, 3, 1, 0, 2, 1, 0, 2, 0, 1, 1, 1, 0, 0, 2, 2, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 0, 2, 1, 1, 1, 0, 0, 2, 1, 1, 3, 0, 1, 1, 0, 1, 0, 3, 2, 2, 0, 2, 0, 1, 1, 1, 0, 0, 0, 2, 3, 2, 0, 0, 0, 2, 2, 3, 2, 1, 2, 3, 0, 0, 2, 0, 0, 0, 0, 1, 1, 2, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 2, 2, 1, 1, 0, 1, 1, 2, 1, 0, 1, 1, 1, 0, 1, 1, 2, 2, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 2, 0, 0, 2, 0, 2, 2, 1, 2, 0, 2, 0, 1, 1, 2, 1, 1, 2, 1, 0, 0, 2, 1, 2, 2, 2, 1, 2, 1, 1, 0, 2, 1, 2, 2, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 0, 0, 2, 1, 2, 1, 2, 1, 1, 0, 3, 1, 0, 1, 1, 0, 3, 0, 1, 2, 0, 3, 1, 0, 0, 2, 0, 0, 1, 1, 1, 1, 0, 1, 0, 2, 0, 1, 0, 2, 1, 1, 1, 1, 1, 3, 2, 0, 0, 3, 1, 3, 0, 2, 0, 1, 1, 0, 2, 0, 1, 1, 2, 0, 1, 2, 0, 0, 1, 0, 0, 0, 1, 2, 1, 0, 1, 0, 2, 1, 1, 2, 1, 0, 1, 0, 0, 0, 2, 0, 0, 0, 2, 0, 1, 2, 0, 2, 2, 2, 0, 0, 0, 2, 2, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 2, 2, 0, 3, 2, 1, 2, 1, 0, 1, 1, 1, 1, 0, 2, 0, 3, 0, 0, 2, 1, 1, 0, 4, 1, 0, 1, 1, 1, 0, 0, 1, 3, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 3, 0, 1, 1, 2, 0, 0, 0, 2, 0, 1, 2, 0, 1, 2, 1, 1, 2, 1, 2, 0, 0, 2, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 1, 1, 0, 2, 3, 1, 1, 2, 1, 0, 1, 1, 1, 2, 1, 1, 1, 1, 0, 1, 2, 1, 1, 1, 2, 2, 0, 1, 1, 0, 2, 0, 1, 0, 0, 0, 2, 2, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 3, 1, 1, 0, 0, 0, 0, 0, 1, 3, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 1, 1, 0, 2, 1, 3, 0, 2, 1, 1, 0, 1, 1, 1, 0, 0, 2, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 2, 0, 1, 1, 1, 2, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 2, 3, 0, 1, 2, 1, 1, 1, 0, 1, 2, 1, 0, 1, 0, 2, 1, 2, 0, 1, 1, 1, 1, 1, 2, 1, 0, 2, 1, 2, 3, 1, 3, 1, 0, 1, 0, 1, 2, 2, 3, 1, 1, 1, 1, 1, 1, 0, 2, 1, 0, 1, 2, 1, 1, 1, 1, 1, 1, 3, 0, 1, 1, 0, 2, 1, 2, 2, 0, 2, 2, 2, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 0, 3, 2, 0, 1, 1, 2, 0, 2, 1, 2, 1, 1, 1, 1, 0, 2, 2, 1, 2, 1, 1, 2, 1, 2, 0, 0, 0, 1, 3, 0, 1, 0, 2, 1, 1, 2, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 3, 0, 0, 1, 2, 0, 2, 1, 0, 3, 0, 1, 0, 2, 1, 3, 0, 2, 1, 1, 0, 1, 1, 1, 1, 2, 0, 2, 1, 0, 1, 0, 0, 0, 2, 2, 1, 3, 1, 3, 2, 1, 1, 1, 0, 1, 0, 2, 1, 0, 0, 0, 3, 2, 1, 1, 0, 1, 1, 1, 1, 1, 2, 3, 1, 0, 3, 2, 2, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 2, 2, 3, 1, 1, 2, 1, 0, 1, 1, 0, 2, 1, 0, 0, 2, 1, 0, 2, 1, 2, 3, 0, 0, 0, 1, 1, 0, 1, 1, 2, 1, 1, 1, 2, 0, 1, 1, 1, 2, 1, 2, 3, 0, 1, 0, 1, 1, 0, 1, 1, 1, 2, 1, 0, 2, 1, 2, 0, 2, 1, 1, 2, 1, 0, 0, 2, 1, 1, 2, 1, 2, 1, 3, 0, 1, 0, 1, 1, 0, 1, 2, 1, 0, 1, 0, 3, 1, 1, 1, 2, 0, 2, 1, 2, 2, 0, 2, 2, 0, 1, 2, 2, 0, 1, 0, 0, 2, 1, 2, 1, 2, 2, 0, 1, 2, 2, 0, 0, 2, 0, 1, 0, 2, 1, 1, 2, 1, 1, 2, 0, 0, 1, 2, 1, 0, 1, 2, 2, 0, 1, 0, 0, 0, 2, 1, 1, 2, 1, 1, 0, 2, 2, 2, 0, 1, 2, 1, 0, 1, 0, 2, 0, 0, 3, 1, 0, 0, 2, 2, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 2, 0, 1, 2, 1, 2, 1, 2, 1, 4, 2, 1, 2, 1, 1, 1, 2, 0, 1, 1, 0, 2, 2, 0, 1, 2, 2, 1, 0, 2, 4, 0, 0, 3, 0, 0, 1, 1, 1, 0, 1, 1, 3, 2, 0, 1, 0, 1, 1, 0, 0, 3, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 3, 1, 1, 0, 0, 1, 1, 0, 1, 2, 0, 1, 2, 0, 3, 1, 0, 1, 1, 2, 2, 2, 2, 1, 1, 1, 3, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 4, 0, 1, 1, 2, 1, 0, 4, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 2, 0, 2, 2, 2, 3, 2, 1, 0, 2, 1, 1, 1, 1, 2, 2, 0, 1, 1, 0, 1, 3, 2, 1]

And finally let’s visualize the sample. In order to do this, let us define a chart using the plotters crate.

:dep plotters
use plotters::prelude::*;

fn plot_histogram(samples: &[usize], filename: &str) {
    let max_value = *samples.iter().max().unwrap_or(&0);
    let frequencies = (0..=max_value)
        .map(|value| samples.iter().filter(|&&x| x == value).count() as u32)
        .collect::<Vec<_>>();

    let root = BitMapBackend::new(filename, (1600, 1200)).into_drawing_area();
    root.fill(&WHITE).unwrap();

    let mut chart = ChartBuilder::on(&root)
        .margin(10)
        .x_label_area_size(40)
        .y_label_area_size(40)
        .caption("Sample Frequencies", ("sans-serif", 30).into_font())
        .build_cartesian_2d(0..max_value, 0..*frequencies.iter().max().unwrap_or(&0))
        .unwrap();

    chart
        .configure_mesh()
        .x_desc("Sample Values")
        .y_desc("Frequencies")
        .draw()
        .unwrap();

    chart
        .draw_series(
            (0..=max_value)
                .map(|x| {
                    let freq = frequencies[x];
                    Rectangle::new(
                        [(x as usize, 0), ((x + 1) as usize, freq)],
                        BLUE.filled(),
                    )
                }),
        )
        .unwrap()
        .label("Frequency")
        .legend(|(x, y)| Rectangle::new([(x, y - 10), (x + 20, y)], BLUE.filled()));

    chart
        .configure_series_labels()
        .border_style(&BLACK)
        .background_style(&WHITE)
        .draw()
        .unwrap();
}

Let’s make the plot.

plot_histogram(&samples, "histogram.png");