Notes on Order Theory

Fundamentals

This section provides an overview of some fundamental concepts in order theory.

Essential Definitions and Examples

Definition

A partial order is a pair \((X, \leq)\) composed of a set \(X\) called the ground set and \(\leq\) is a binary relation with the following relation: - reflexivity: \(x \leq x\ \forall x \in X\) - transitivity: \(x \leq y \land y \leq z \implies x \leq z\ \forall x,y,z \in X\) - antisymmtry: \(x \leq y \land y \leq x \implies x = y\ \forall x,y \in X\)

Let us consider an example of a partial order and some of the ways we can represent them.

Example

Let \(X = \{a, b, c, d, e \}\), then we might have a partial order \(\\{(a,a), (a,c), (a,e), (b,b), (b,c), (b,d), (b,e), (c,c), (d,d), (d,e), (e,e)\\}\). This partial order can be represented as a matrix.

\[\begin{array}{c c} & \begin{array}{c c c c c} a & b & c & d & e \\ \end{array} \\ \begin{array}{c c c c c} a \\ b \\ c \\ d \\ e \\ \end{array} & \left[ \begin{array}{c c c c c} 1 & 0 & 1 & 0 & 1 \\ & 1 & 1 & 1 & 1 \\ & & 1 & 0 & 0 \\ & \huge 0 & & 1 & 1 \\ & & & & 1 \\ \end{array} \right] \end{array} \]

Another representation is a directed graph (AKA a digraph):

from graphviz import Digraph
XxX = 'aa', 'ac', 'ae', 'bb', 'bc', 'bd', 'be', 'cc', 'dd', 'de', 'ee'
D = Digraph('example_partial_order')
for xx in XxX:
    D.edge(xx[0], xx[1])
D

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/backend/execute.py:76, in run_check(cmd, input_lines, encoding, quiet, **kwargs)
     75         kwargs['stdout'] = kwargs['stderr'] = subprocess.PIPE
---> 76     proc = _run_input_lines(cmd, input_lines, kwargs=kwargs)
     77 else:

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/backend/execute.py:96, in _run_input_lines(cmd, input_lines, kwargs)
     95 def _run_input_lines(cmd, input_lines, *, kwargs):
---> 96     popen = subprocess.Popen(cmd, stdin=subprocess.PIPE, **kwargs)
     98     stdin_write = popen.stdin.write

File /usr/lib/python3.12/subprocess.py:1026, in Popen.__init__(self, args, bufsize, executable, stdin, stdout, stderr, preexec_fn, close_fds, shell, cwd, env, universal_newlines, startupinfo, creationflags, restore_signals, start_new_session, pass_fds, user, group, extra_groups, encoding, errors, text, umask, pipesize, process_group)
   1023             self.stderr = io.TextIOWrapper(self.stderr,
   1024                     encoding=encoding, errors=errors)
-> 1026     self._execute_child(args, executable, preexec_fn, close_fds,
   1027                         pass_fds, cwd, env,
   1028                         startupinfo, creationflags, shell,
   1029                         p2cread, p2cwrite,
   1030                         c2pread, c2pwrite,
   1031                         errread, errwrite,
   1032                         restore_signals,
   1033                         gid, gids, uid, umask,
   1034                         start_new_session, process_group)
   1035 except:
   1036     # Cleanup if the child failed starting.

File /usr/lib/python3.12/subprocess.py:1955, in Popen._execute_child(self, args, executable, preexec_fn, close_fds, pass_fds, cwd, env, startupinfo, creationflags, shell, p2cread, p2cwrite, c2pread, c2pwrite, errread, errwrite, restore_signals, gid, gids, uid, umask, start_new_session, process_group)
   1954 if err_filename is not None:
-> 1955     raise child_exception_type(errno_num, err_msg, err_filename)
   1956 else:

FileNotFoundError: [Errno 2] No such file or directory: PosixPath('dot')

The above exception was the direct cause of the following exception:

ExecutableNotFound                        Traceback (most recent call last)
File ~/projects/blog/venv/lib/python3.12/site-packages/IPython/core/formatters.py:1036, in MimeBundleFormatter.__call__(self, obj, include, exclude)
   1033     method = get_real_method(obj, self.print_method)
   1035     if method is not None:
-> 1036         return method(include=include, exclude=exclude)
   1037     return None
   1038 else:

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/jupyter_integration.py:98, in JupyterIntegration._repr_mimebundle_(self, include, exclude, **_)
     96 include = set(include) if include is not None else {self._jupyter_mimetype}
     97 include -= set(exclude or [])
---> 98 return {mimetype: getattr(self, method_name)()
     99         for mimetype, method_name in MIME_TYPES.items()
    100         if mimetype in include}

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/jupyter_integration.py:112, in JupyterIntegration._repr_image_svg_xml(self)
    110 def _repr_image_svg_xml(self) -> str:
    111     """Return the rendered graph as SVG string."""
--> 112     return self.pipe(format='svg', encoding=SVG_ENCODING)

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/piping.py:104, in Pipe.pipe(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
     55 def pipe(self,
     56          format: typing.Optional[str] = None,
     57          renderer: typing.Optional[str] = None,
   (...)
     61          engine: typing.Optional[str] = None,
     62          encoding: typing.Optional[str] = None) -> typing.Union[bytes, str]:
     63     """Return the source piped through the Graphviz layout command.
     64 
     65     Args:
   (...)
    102         '<?xml version='
    103     """
--> 104     return self._pipe_legacy(format,
    105                              renderer=renderer,
    106                              formatter=formatter,
    107                              neato_no_op=neato_no_op,
    108                              quiet=quiet,
    109                              engine=engine,
    110                              encoding=encoding)

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/_tools.py:171, in deprecate_positional_args.<locals>.decorator.<locals>.wrapper(*args, **kwargs)
    162     wanted = ', '.join(f'{name}={value!r}'
    163                        for name, value in deprecated.items())
    164     warnings.warn(f'The signature of {func.__name__} will be reduced'
    165                   f' to {supported_number} positional args'
    166                   f' {list(supported)}: pass {wanted}'
    167                   ' as keyword arg(s)',
    168                   stacklevel=stacklevel,
    169                   category=category)
--> 171 return func(*args, **kwargs)

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/piping.py:121, in Pipe._pipe_legacy(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
    112 @_tools.deprecate_positional_args(supported_number=2)
    113 def _pipe_legacy(self,
    114                  format: typing.Optional[str] = None,
   (...)
    119                  engine: typing.Optional[str] = None,
    120                  encoding: typing.Optional[str] = None) -> typing.Union[bytes, str]:
--> 121     return self._pipe_future(format,
    122                              renderer=renderer,
    123                              formatter=formatter,
    124                              neato_no_op=neato_no_op,
    125                              quiet=quiet,
    126                              engine=engine,
    127                              encoding=encoding)

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/piping.py:149, in Pipe._pipe_future(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
    146 if encoding is not None:
    147     if codecs.lookup(encoding) is codecs.lookup(self.encoding):
    148         # common case: both stdin and stdout need the same encoding
--> 149         return self._pipe_lines_string(*args, encoding=encoding, **kwargs)
    150     try:
    151         raw = self._pipe_lines(*args, input_encoding=self.encoding, **kwargs)

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/backend/piping.py:212, in pipe_lines_string(engine, format, input_lines, encoding, renderer, formatter, neato_no_op, quiet)
    206 cmd = dot_command.command(engine, format,
    207                           renderer=renderer,
    208                           formatter=formatter,
    209                           neato_no_op=neato_no_op)
    210 kwargs = {'input_lines': input_lines, 'encoding': encoding}
--> 212 proc = execute.run_check(cmd, capture_output=True, quiet=quiet, **kwargs)
    213 return proc.stdout

File ~/projects/blog/venv/lib/python3.12/site-packages/graphviz/backend/execute.py:81, in run_check(cmd, input_lines, encoding, quiet, **kwargs)
     79 except OSError as e:
     80     if e.errno == errno.ENOENT:
---> 81         raise ExecutableNotFound(cmd) from e
     82     raise
     84 if not quiet and proc.stderr:

ExecutableNotFound: failed to execute PosixPath('dot'), make sure the Graphviz executables are on your systems' PATH

<graphviz.graphs.Digraph at 0x798deac5e390>

Tip

The previous example only required a relatively small subset of the Cartesian \(X \times X\). When you a have too many elements in \(X\) to deal with by hand, one quick Python script to make the pairs in a format suitable for \(\LaTeX\) is the following:

from itertools import product
X = 'a', 'b', 'c', 'd', 'e'
XxX = ['('+', '.join(i) + ')' for i in product(X,X)]
XxX = sorted(XxX)
XxX = str(XxX).replace("'", "")
XxX = XxX.replace("[", "\\\\{")
XxX = XxX.replace("]", "\\\\}")
print(XxX)

\\{(a, a), (a, b), (a, c), (a, d), (a, e), (b, a), (b, b), (b, c), (b, d), (b, e), (c, a), (c, b), (c, c), (c, d), (c, e), (d, a), (d, b), (d, c), (d, d), (d, e), (e, a), (e, b), (e, c), (e, d), (e, e)\\}

Definition

A strict partial order is a pair \((X, <)\) composed of a set \(X\) called the ground set and \(<\) is a binary relation with the following relation: - transitivity: \(x < y \land y < z \implies x < z\ \forall x,y,z \in X\) - asymmetry: \(\lnot (x < y \land y < x) \ \forall x,y \in X\)

Proposition

The digraph representation of a strict order is a directed acyclic graph (DAG).

Often we can start with a strict order and derive similar results for a corresponding (non-strict) partial order.

Definition

\(\{x, y\}\) are a comparable pair if \(x < y \lor y > x\), denoted \(x \sim y\).

Definition

A graph \(G = (V, E)\) whose edge set \(E\) is the set of comparable pairs of a partial order is called the comparability graph.

Example

Suppose we have the strict partial order \(\\{(a,c), (a,e), (b,c), (b,d), (b,e), (d,e)\\}\), then its comparability graph would look like:

flowchart TB
    a o--o c
    a o--o e
    b o--o c
    b o--o d
    b o--o e
    d o--o e

flowchart TB
    a o--o c
    a o--o e
    b o--o c
    b o--o d
    b o--o e
    d o--o e

Definition

\(\{x, y\}\) are an incomparable pair if \(\lnot (x < y \lor y > x)\), denoted \(x \parallel y\).

Definition

A graph \(G = (V, E)\) whose edge set \(E\) is the set of incomparable pairs of a partial order is called the comparability graph.

Example Suppose we have the strict partial order \(\\{(a,c), (a,e), (b,c), (b,d), (b,e), (d,e)\\}\), then its incomparability graph (AKA cocomparability graph) would look like:

flowchart TB
    a o--o b
    a o--o d
    c o--o d
    c o--o e

flowchart TB
    a o--o b
    a o--o d
    c o--o d
    c o--o e

Proposition

The edge set of an incomparability graph is the complement of the edge set of the comparability graph.

Definition

A cover relation \(x \prec y\) is satisfied when \(x < y\) and there does not exist \(z\) such that \(x < z < y\).

Definition

A graph \(G = (V, E)\) is a cover graph when its edge set \(E\) is a collection of pairs satisfying a cover relation.

Example Suppose we have the strict partial order \(\\{(a,c), (a,e), (b,c), (b,d), (b,e), (d,e)\\}\), then its cover graph would look like:

flowchart TB
    a o--o c
    a o--o e
    b o--o c
    b o--o d
    d o--o e

flowchart TB
    a o--o c
    a o--o e
    b o--o c
    b o--o d
    d o--o e

Definition

A directed graph \(D = (V, E)\) is a directed cover graph when its edge set \(E\) is a collection of pairs satisfying a cover relation and the order of the pairs is represented with arcs.

Example

Suppose we have the strict partial order \(\\{(a,c), (a,e), (b,c), (b,d), (b,e), (d,e)\\}\), then its directed cover graph would look like:

flowchart TB
    e --> a
    e --> d
    c --> a
    c --> b
    d --> b

flowchart TB
    e --> a
    e --> d
    c --> a
    c --> b
    d --> b

Definition

A cover diagram is a drawing of the directed graph representing a cover relation such that the edges are cover pairs \((x,y)\). Edges are drawn in such a way that \(x\) is below \(y\) (in the graph embedding) ad the edge is \(y\)-monotone.

Example

Suppose we have the strict partial order \(\\{(a,c), (a,e), (b,c), (b,d), (b,e), (d,e)\\}\), then its cover diagram would look like:

import matplotlib.pyplot as plt
import networkx as nx
import warnings

g = nx.Graph()

g.add_edge('a', 'c')
g.add_edge('a', 'e')
g.add_edge('b', 'c')
g.add_edge('b', 'd')
g.add_edge('d', 'e')

pos = {'a':(0,1),
       'b':(1,0),
       'c':(0,3),
       'd':(2,2),
       'e':(1,4)}

with warnings.catch_warnings():
    warnings.filterwarnings('ignore')
    nx.draw(g, pos=pos, labels={i:i for i in g.nodes()}, node_color=(0.5,)*3)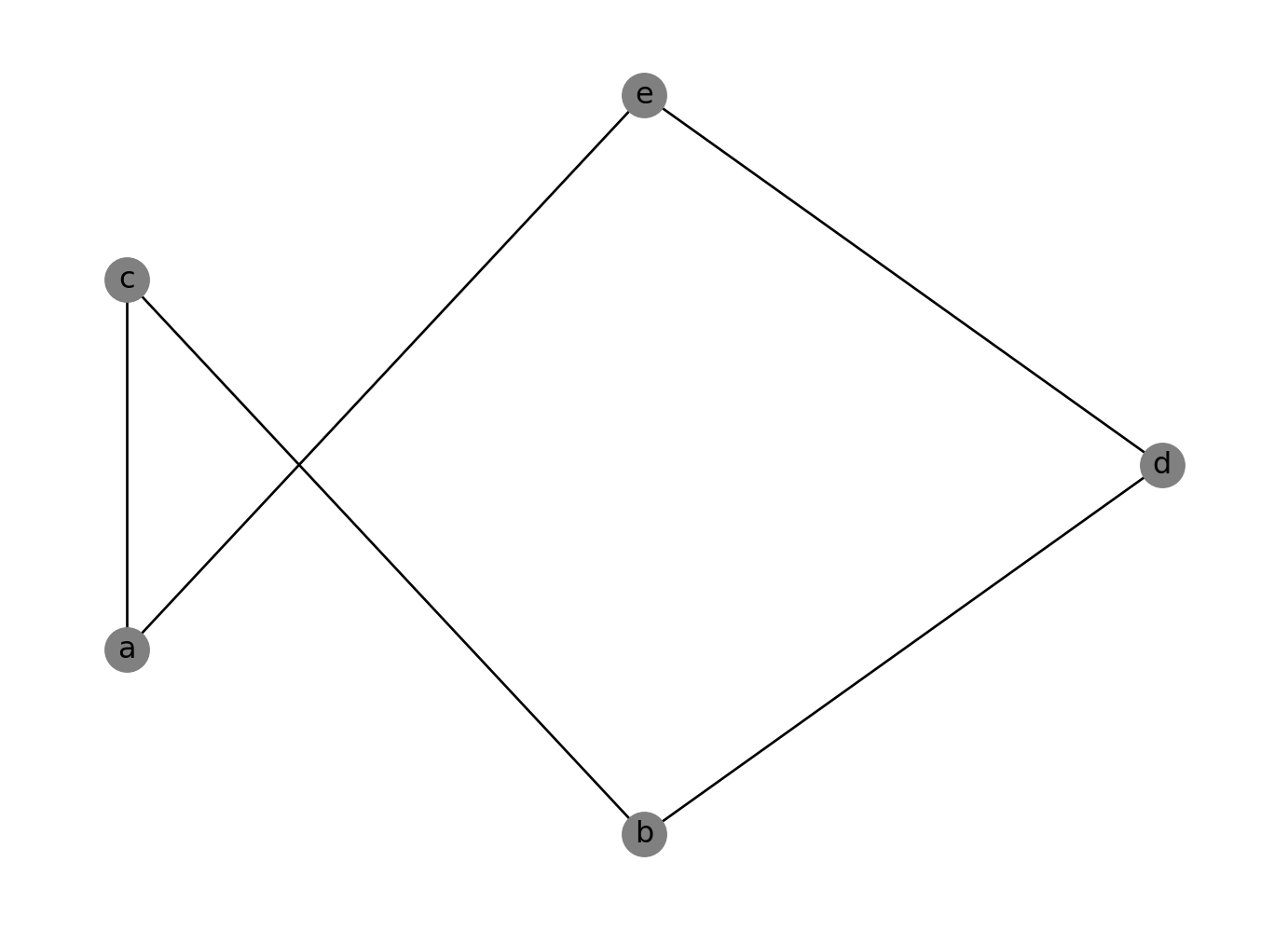

Special Classes of Orders

• linear orders (aka total orders, aka chains).
  • Important in computer science problems such as sorting.
  • Important in mathematics for defining sets of numbers such as \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{R}\) and others.
• Boolean lattices
  • \(B_n = (2^{[n]}, \subseteq )\) where \[[n] = \{ 1, \ldots, n \}\]
  • Looks at subsets of \(n\) ordered by inclusion

Proposition

The subset relation on any family of sets is an order relation.

Example

Intervals, discs, balls, subtrees, subgraphs, subgroups are all included sets under the order relation of set inclusion.

Definition

A containment relation is […]

Definition

For \(A \subseteq X\) we have the down-set of \(A\) being \[D[A] = \bigcup_{a \in A} D[a] = \{ x | \exists a \in A\ \text{s.t.}\ x \leq a \}\].

Proposition

Every finite order is the containment order of a family of sets.

Proof Let \(P = (X, \leq)\) be an order relation.

For \(a \in X\) let \(D[a] = \{ x : x \leq a \}\) be the down-set of a.

Let \[y = \{ D[a] : a \in X \}\].

Now we claim that \(P \cong (y, \subseteq )\) where \(\cong\) is an order-preserving isomorphism.

Since isomorphisms are bijections, we take the bijection in this case to \(D : x \mapsto D[x]\).

We need to verify that \(D\) as we have just defined it is actually a bijection.

If a mapping is a bijection, then it is both injective and surjective.

Considering the injective case, let take two elements \(x\) and \(y\) such that \(x \neq y\) then there are three possibilities: - \(x < y \implies y \not\in D[x]\) - \(x > y \implies x \not\in D[y]\) - \(x \parallel y\) (i.e. \(x\) and \(y\) are not comparable in the order) which implies \((y \not\in D[x]) \land (x \not\in D[y])\)

Surjectivity is given by definition of \(D\).

And we have that \(D\) is order-preserving in the sense that \(x \leq y \iff D[x] \subseteq D[y]\). \[\blacksquare\]

Definition

A lower bound of a subset \(S\) of partially ordered set \((P, \leq)\) is an element \(a \in P\) such that \(a \leq x \forall x \in S\).

Definition

A lower bound \(a \in S\) is called an infinum (or greatest lower bound, or meet) of \(S\) if for all lower bounds \(y \in S\) we have \(y \leq a\).

Definition

An upper bound of a subset \(S\) of partially ordered set \((P, \leq)\) is an element \(b \in P\) such that \(b \geq x \forall x \in S\).

Definition

An upper bound \(b\) of \(S\) is called a supremum (or least upper bound, or join) of \(S\) if for all upper bounds \(z \in S\) we have \(z \leq b\).

Definition

A finite poset on \(S\) is a lattice if every subset of \(S\) has an unique least upper bound (aka join or supremum) denoted \(\lor\) and an unique greatest lower bound (aka meet or infinum) denoted \(\land\).

Definition

The down-set lattice of \(P\) given by \[D(P) = (\{ D[A] : A \subset X \}, \subseteq)\].

Definition

A lattice \((L, \lor, \land)\) is distributive if the following identity holds for all \(x,y,z \in L\):

\[x \land (y \lor z) = (x \land y) \lor (x \land z)\]

where \(\land\) and \(\lor\) are the meet and join operations.

Proposition

The down-set lattice of \(P\) is a distributive lattice.

Proof (Hint) Take \(\lor\) to be \(\cup\) and \(\land\) to be \(\cap\).

Definition

\(Q = (Y, \leq_Q )\) is a subposet of \(P = (X, \leq_P)\) if \(Y \subseteq X\) and \((\leq_Q) = (\leq_P) \cap (Y \times Y)\).

References

• Lectures: Introduction to Order Theory, Fall 2020
• Introduction to Order Theorie
• Introduction to order theory
• Infinum and Supremum